Issues of Proof of Stake
While proof of stake has some promising advantages, as described above, some issues need to be solved to create a safe PoS blockchain.
Nothing at stake
The so-called nothing at stake problem was already described in 2014 by Vitalik Buterin.
Let’s again consider a proof of work blockchain. If an attacker wants to create an alternative chain, he must split his hardware and electricity resources among both chains. He can’t mine on each of the chains with 100% of his resources.
In proof of stake, things look different. After a fork, funds exist on both branches. Hence, the attacker can validate on both branches. The following diagram gives a numerical example.
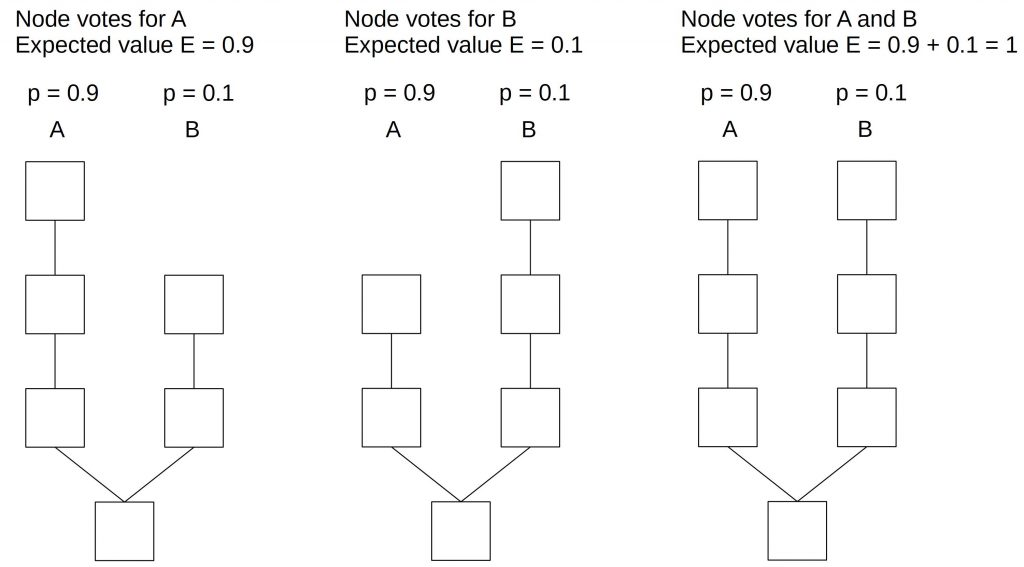
In the situation above, we have a chain that splits into branches A and B. Branch A will be successful with the likelihood of 0.9 and branch B with the likelihood of 0.1. A node (block producer) can now decide to vote on branch A or branch B or both. If we have a block reward of 1 coin a node (block producer) that votes only on branch A will have an expected return of 0.9 * 1 = 0.9. If it votes only on branch B, the expected value is 0.1*1 = 0.1. And since voting on both branches doesn’t impose any additional costs, the expected value for voting on both branches is 0.9*1+0.1*1 = 1. Hence, it is beneficial for a block producer to vote on both branches instead of deciding on one.
Literally, there is nothing at stake.
The consequence is that each branch will have the same length (and weight) and therefore, the network won’t reach a consensus on which chain the correct one is.
A remedy to the nothing at stake problem can be the introduction of penalties.
The first scheme could penalize nodes that vote simultaneously (the same block height) on both chains. Let’s assume that the penalty is 5 coins.
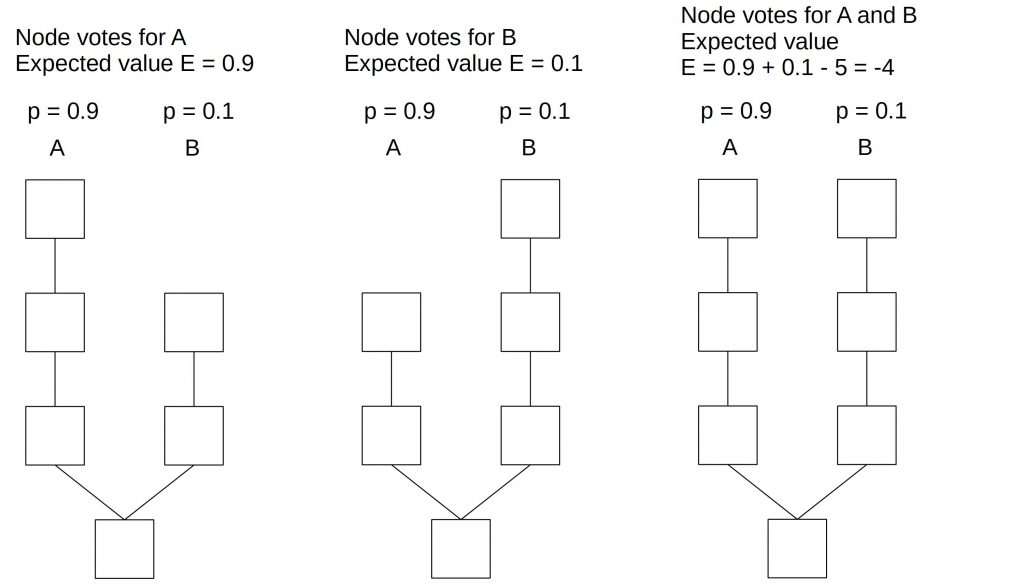
In the first two cases, the block producer suffers no penalty. But in the third case where he votes on chains A and B, he gets penalized by burning his deposit (or a fraction of it). The expected loss on both chains is 0.9*-5 + 0.1*-5=-5. If he receives a block reward, the total expected value is 1-5=-4.
This would be less profitable than voting only on-chain A or chain B.
This approach has two issues:
- The block producers must be selected well ahead of time. Otherwise, the chance of being selected as a block producer for the same block height on both branches is rather low.
- Determining block producers a long time before they are allowed to vote creates the risk of block producer collusion.
Another way to introduce penalties would be to punish every block producer that votes on the “wrong” chain. The wrong chain here means any other chain.
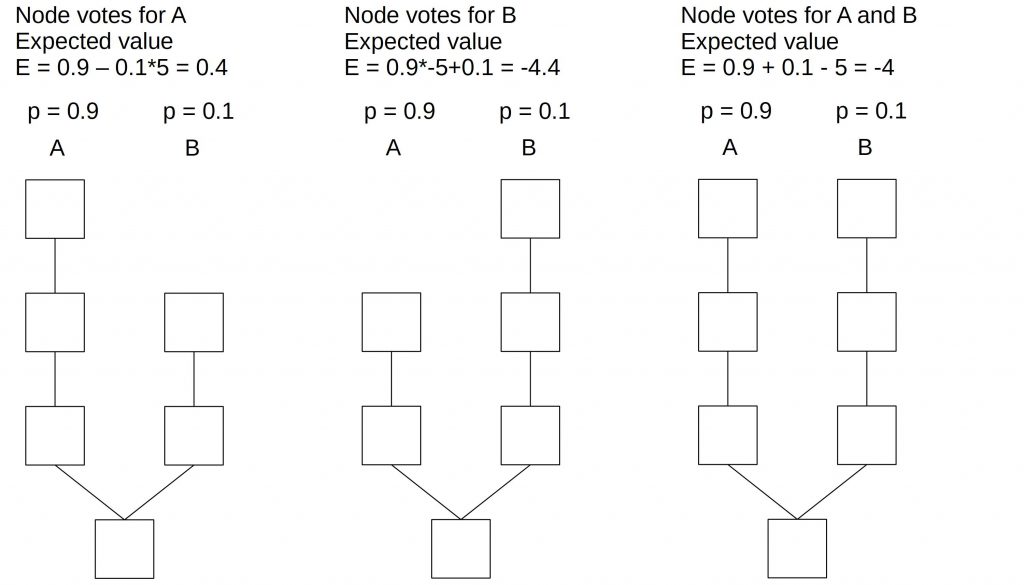
If the block producer votes on chain A, he receives a punishment on chain B. Its expected value is then 0.4. If the block producer chooses to vote only on chain B, he receives a punishment on chain A and suffers a loss of -4.4. If voting on both chains, the loss is -4.
In this example, it would be beneficial for the block producer to vote only on-chain A since this promises the highest return.
But if we change the numbers, it could be beneficial for block producers not to vote at all.
Penalty: 5
pA = 0.4
pB = 0.6
Voting on A: 0.6 – 0.4*5 = -1.4
Voting on B: 0.6 * -5 + 0.4 = -2.6
Voting on A and B: 0.6+0.6*-5+0.4+0.6*-5=-4
Voting on neither A nor B: 0
The fourth option, not voting at all, is the one with the highest expected return.
Long-range Attacks
Another problem with penalties is that they need to be enforced somehow. This is only possible if a block producer locked up a deposit that can be destroyed in the case of misbehavior. But the deposit cannot be kept forever. After a while, block producers want it back. After the deposit is released, there is nothing at stake if validating on an earlier branch.
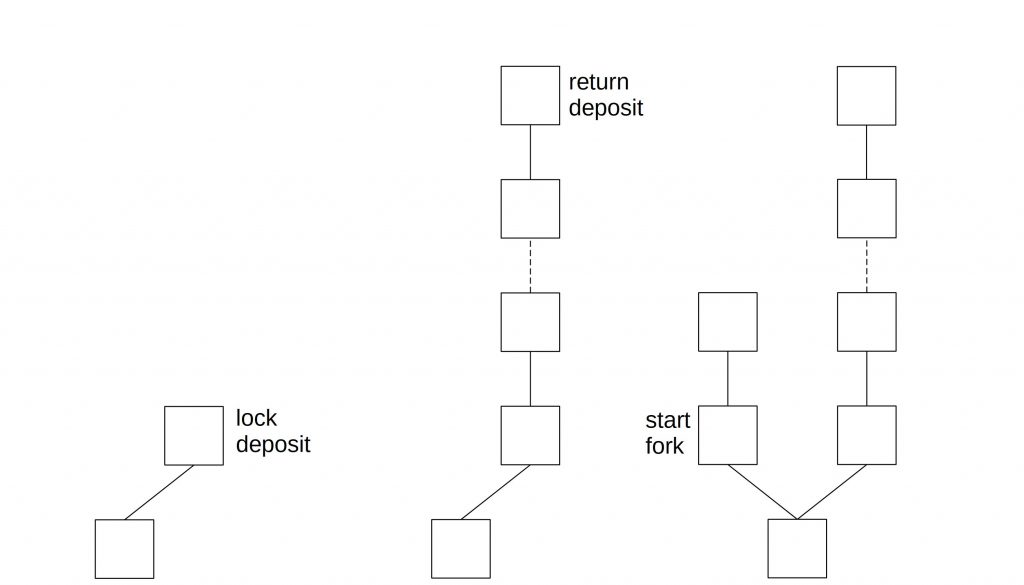
In the situation above, an attacker locks its deposit and after a certain number of blocks, he receives it back. After that, he starts the fork.
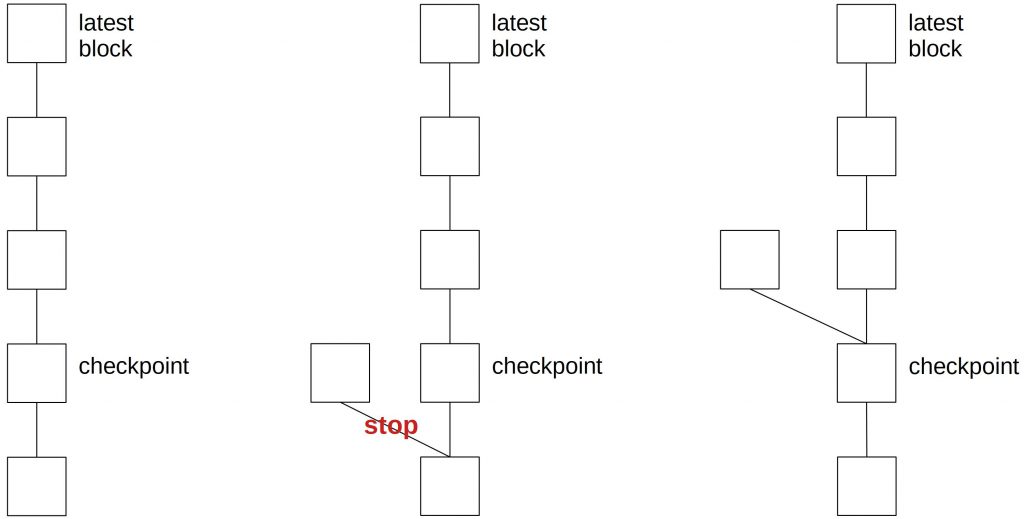
A countermeasure is checkpoints. If a checkpoint is created, a node doesn’t accept forks that start before this checkpoint.
