Randomness Generation
When explaining the simulated mining rig, we needed a random element to avoid stake grinding. Creating random numbers in a decentralized manner is difficult since it must be verifiable. In most cases, an approach with multiple contributors is chosen.
Here, you will learn two methods of how to create a distributed, verifiable random function.
2 Phase Commit Reveal Scheme
In the two-phase commit reveal scheme, all participants think of a secret random number r. Then they calculate the hash of it and by including a salt and publish the hash. This is the first phase (commit).
In the second phase (reveal), the participants publish their secret number r and the salt. If the r and salt result in the same hash this participant committed, then it is processed further. Otherwise, it is ignored. All valid r’s then become the input of another hash function, and the output is our random number.
But there is a problem. The last actor in the reveal phase can calculate the result before all other participants. This gives him an advantage and he can decide to not reveal his r. This problem is called the last actor problem.
In order to solve this, a deposit in the commit phase is required which is returned if the participant is honest in the reveal phase.
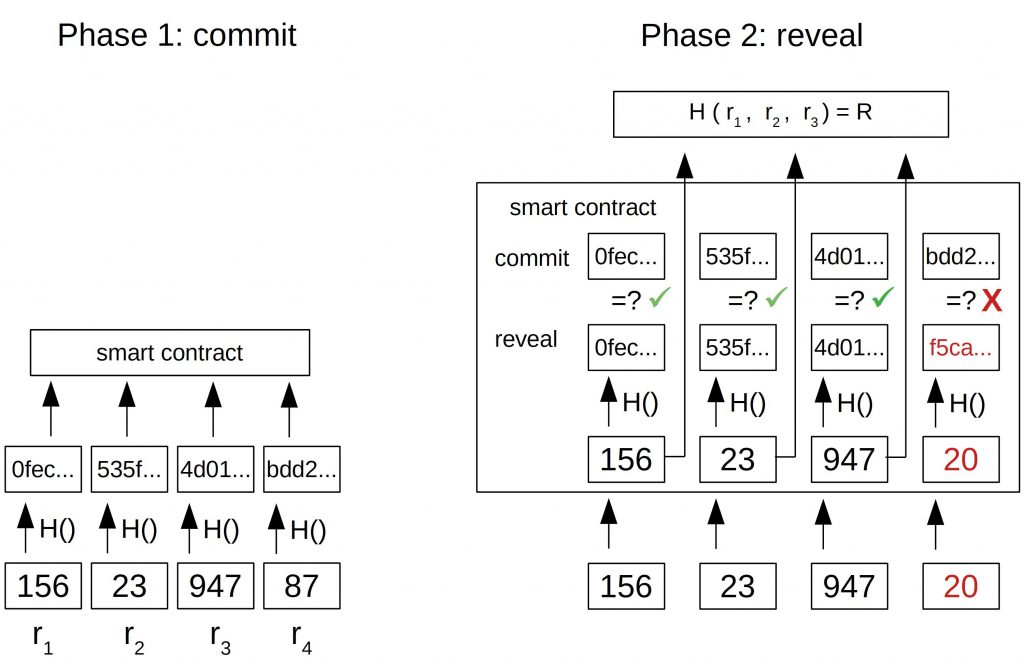
The deposit is only an incentive for being honest. If the gain from not publishing the r is higher than the deposit’s loss, this scheme doesn’t work.
A high deposit, however, is a barrier for participants to contribute to the random number generation.
Low influence function
Another approach is to minimize the influence a participant has on the resulting random number. This is done by splitting all participants into groups.
Now, each participant submits either 0 or 1. Then the occurrence of all 0 and 1 in each group is counted. If in a group are more 0 than 1, this group submits a 0. If there are more 1 than 0 then it submits a 1.
Once all groups calculated their result, all results are concatenated to one big binary random number.
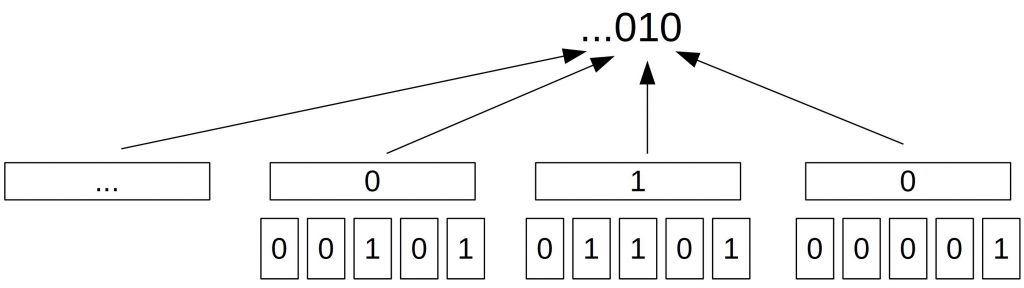
If a user decides not to participate, he needs to change the majority of his group. And even if he manages this, he changes only one bit in the result.
