Sparse Merkle Tree (SMT)
In a Sparse Merkle Tree (SMT), the position of the data in the leaves depends on its content. Let’s assume, we have the following data: 011.
We calculate its position in the sparse Merkle tree by looking at each bit individually from left to right. When it is zero, we use the left path. If it is one, we take the right path. We start with the left bit (0). Since it is zero, we go left. The next bit is 1, so we take the right path in the next level. The next bit is again 1, so we take the right path again.

A sparse Merkle tree (SMT) can be used to prove that a certain piece of data is not included in the Merkle tree. The location of the leaf and the content of the leaf are bound together. This means, a SMT is an authentic key value store.
The consequence of this calculation is that depending on the size of the data many leaves will be empty. The following figure shows a sparse Merkle tree with only two leaves filled. Empty leaves do not need to be stored. Another consequence is that the root hash does not depend on the order in which the leaves are inserted (as the order depends solely on the data itself).
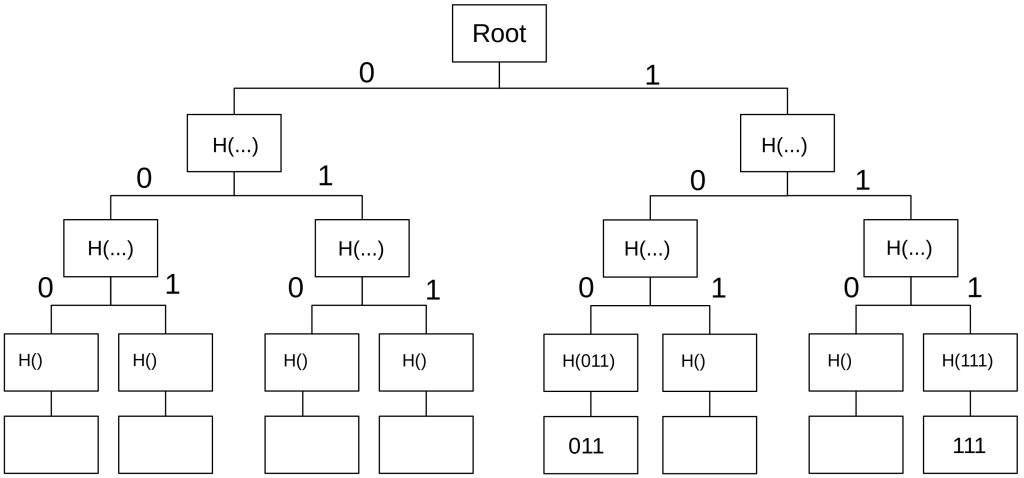
The depth of a sparse Merkle tree depends on the maximal number of data bits. A tree with 16 bits (2^4) has 4 levels. A tree with data of 256 bits length (2^256) has 256 levels.

