Condorcet Jury Theorem

Published by Mario Oettler on

Game Theory & Blockchain Social Choice Condorcet Jury Theorem

Last Updated on 28. April 2023 by Martin Schuster

The Condorcet Jury theorem answers the question under which circumstances a binary group decision comes to a better conclusion than the decision of a single individual.

For that purpose, we assume:

  • A jury has to decide between option A and option B.
  • The jury consists of k members, whereas k > 2 and odd.
  • Every jury member is likely to choose the better option with a probability of q.
  • The jury decides with an absolute majority.

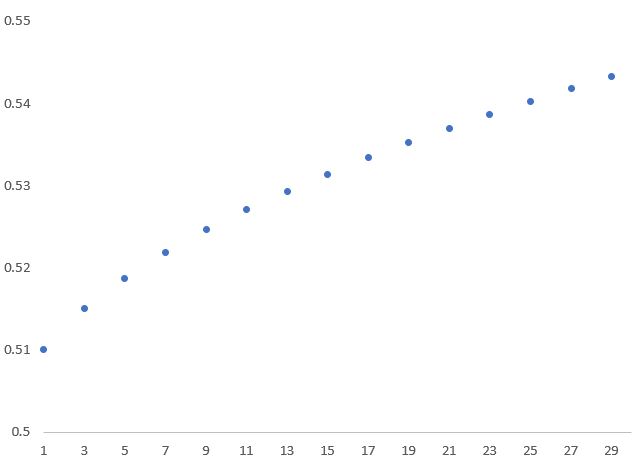
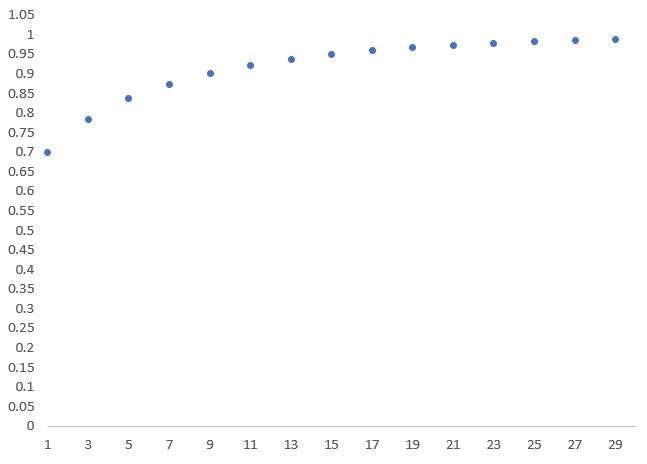
If q is > 0.5, the likelihood that the jury chooses the better option increases with the number of jury members. The following two charts show the increasing likelihood for q = 0.51 and 0.7 depending on the jury size.

Development of the likelihood that the jury’s decision is correct at q  = 0.51, depending on the jury size.
Development of the likelihood that the jury’s decision is correct at q  = 0.7, depending on the jury size.
Previous Topic
Back to Lesson
Next Topic
Categories: