Price of Anarchy
Last Updated on 28. April 2023 by Martin Schuster
The price of anarchy compares the efficiency of a mechanism (or algorithm) in the case of selfish behavior with the efficiency achieved by a centralized authority.
We can consider two cases
1. The game shows the welfare. Then the formula of the price of anarchy is:
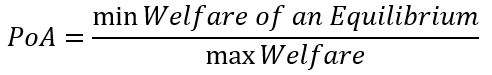
2. The game shows the cost. Then the formula of the price of anarchy is:
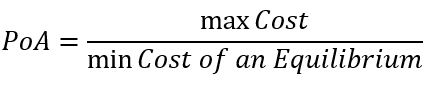
The welfare or cost are a function of the utilities of all players. In this function, the individual utilities are aggregated. Most simply, they are added.
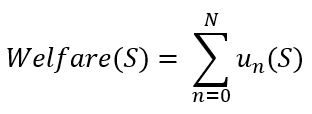
S: strategy combination of all players
ui(S) utility of player i in a specific strategy combination S
N: total number of players
n: player index
Of course, other aggregation functions are possible.
For considering the cost, the formula would be:
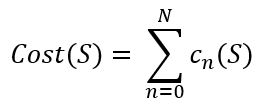
S: strategy combination of all players
ci(S) cost of player i in a certain strategy combination S
N: total number of players
n: player index
Example of Price of Anarchy
In this pay-off matrix, we consider pay-offs (instead of costs).
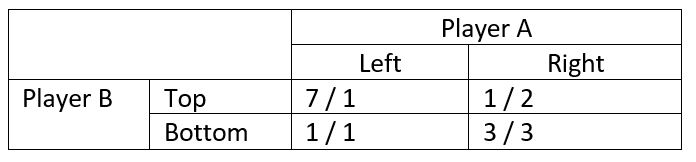
The only Nash equilibrium is {R, B} and yields a total pay-off of 3 + 3 =6, assuming an addition-aggregation function. Since we have only one Nash equilibrium, we take this as the minimal welfare equilibrium.
The maximum total pay-off is in strategy combination {L, T} with 7+1 = 8.
Hence, we get
PoA = 6/8 = 0.75.
The price of anarchy can also be calculated with mixed strategies and mixed equilibria.
Interpretation
If the price of anarchy is
= 1: there is no loss of welfare compared to coordination.
0 > PoA < 1: some portion of the maximum achievable welfare is lost by anarchy.
= 0: is only possible if there is no welfare in the case of anarchy.
Limitations of the Price of Anarchy
In our model, we assume that the system achieves equilibrium. But in some cases, this is not certain. If we consider the following scenario, we see that there are two equilibria yielding the same payoff. But due to coordination errors, both players could choose a strategy combination that leads to a non-equilibrium situation, yielding a lower total payoff than the worst equilibrium.
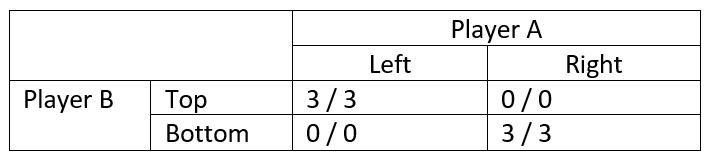
The Nash equilibria exist at {L, T} and {R, B}.
The price of anarchy would be PoA = 3/3 = 1 (No loss).
But without some coordination mechanism, it is not clear whether one of these equilibria will be reached. If the players fail to achieve the equilibrium, the minimal welfare would be 0 and the price of anarchy would be 0/3 = 0 (complete loss).
Another limitation is that the cost for the central coordinating authority is not considered in the equations. This means it overestimates the welfare (or underestimates the cost) for the optimal solution.

 Register
Register Sign in
Sign in