Choice under Risk
If we deal with risk, we know the likelihoods of each situation. The easiest rule is to choose the situation with the highest expected value.
The following table shows the pay-offs and likelihoods of four situations.
| S1 | S2 | S3 | S4 | Expected pay-off | |
| Probability | 0.2 | 0.4 | 0.1 | 0.3 | |
| A1 | 20 | 15 | 20 | 3 | 20*0.2+15*0.4+20*0.1+3*0.3 = 12.9 |
| A2 | 5 | 6 | 7 | 4 | 5.3 |
| A3 | 22 | 3 | 3 | -2 | 5.3 |
A1 is the option with the highest expected value.
The problem is that people have different risk appetites. Some prefer situations with a higher pay-off but a lower probability of occurrence, while others prefer options with a lower pay-off but a higher probability of occurrence.
St. Petersburg Paradox
This can be demonstrated with a game called St. Petersburg Paradox:
The game master throws a coin. If the coin shows head, the pay-off for the participant is doubled. The initial amount is two EUR. (Other examples start with 1 Euro doubling it every round. This would lead to the same conclusion, but at a lower expected value at ½∞.) But if the coin shows tail, the game is stopped and the participant receives nothing. So, if the coin shows three times in a row head, the amount is 2*2*2*2 = 16.
The question is, how much would you pay (bet) to participate in this game? The expected value is infinite:
E = 0.51 * 21 + 0.52*22 + 0.53 * 23 + …
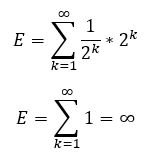
But would anybody really pay an infinite amount to play this game? Or even a smaller amount of 1 million EUR? Probably not.
Ellsberg Paradox
Another experiment shows that the individual perception of risk is not always rational. The experiment is called Ellsberg Paradox.
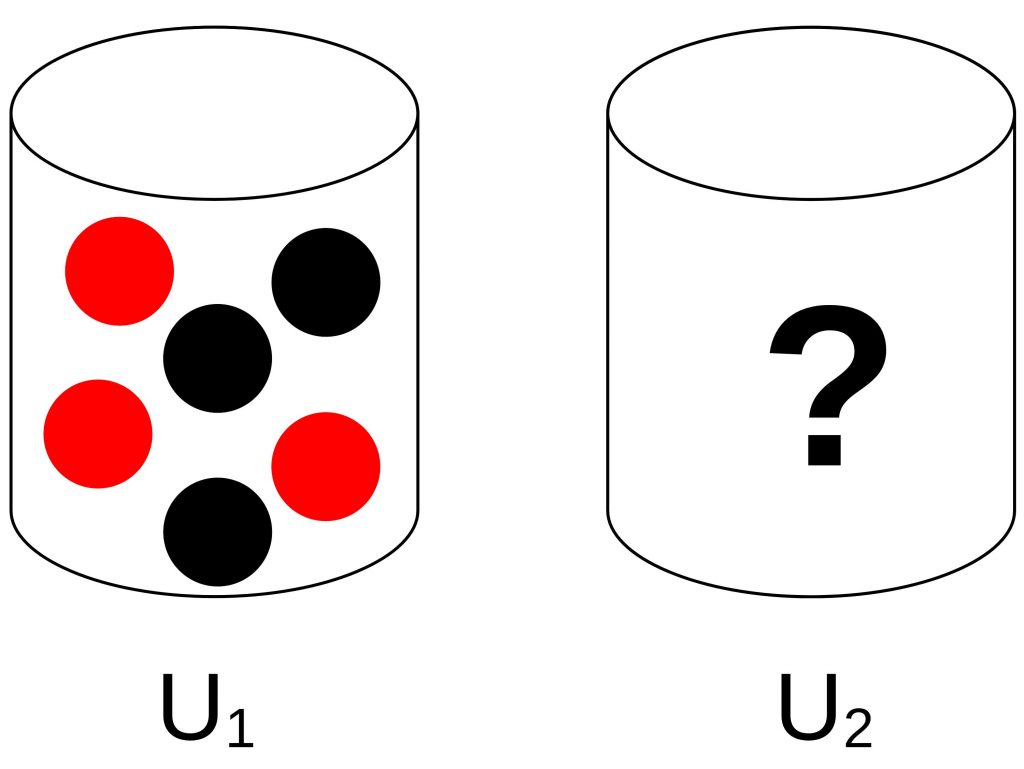
Suppose there are two urns. In urn U1, there are three red balls and three black balls. This information is known to the participant. In the second urn, there are also red and black balls. But their distribution is unknown to the participant. The task is to choose an urn first and then blindly draw a ball from it. If this ball is red, the participant wins a prize.
For both urns, the expected value is the same. For urn 2 every distribution of balls is conceivable. So, in the end, the likelihood of drawing a red ball is equal to drawing a black ball. But for some reason, in reality, people prefer urn 1 to urn 2. This shows that the utility of the expected value is not equal to the expected value of the utilities.
Such utility functions should be taken seriously because they influence rational decisions. If we make mistakes in assigning the pay-offs for the participants in a game, we are likely to get wrong results in our analysis.
