Top Trading Cycle Algorithm
The top trading cycle algorithm (TTCA) is a mechanism to improve the allocation of assets among a group of people. It can be a means in negotiations to reach a consensus about the utility transfer. The TTCA applies to exchange the assets in rounds to maximize the total welfare.
The TTCA is a truthful mechanism. This means the best strategy is to truthfully state its preferences.
Algorithm
There are N children. Each got a random present. Since the allocation is randomly, some kids are not very happy with their present while others got their favorite gift.
Step 1: Each child points to the child who’s present it would like to have instead of its own present. It is possible to point at oneself if there is no better present available.
Step 2: Now, we create a directed graph. Children are nodes, and the pointing is the edges. In this graph, we look for a directed circle.
Step 3: Presents are exchanged in the opposite direction of the circle. Nodes that participated in a circle are removed from the algorithm.
Then continue with step 1. Continue until all children are removed from the algorithm.
Numerical Example of the TTCA
First round:
| Child | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1st choice | 1 | 3 | 4 | 5 | 3 | 1 | 2 |
| 2nd choice | 3 | 5 | 5 | 1 | 7 | 7 | 6 |
| 3rd choice | 4 | 6 | 3 | 3 | 1 | 3 | 3 |
| 4th choice | 6 | 2 | 1 | 4 | 5 | 4 | 1 |
| 5th choice | 5 | 1 | 2 | 2 | 6 | 2 | 5 |
| 6th choice | 2 | 7 | … | … | … | … | … |
| 7th choice | 7 | 4 | … | … | … | … | … |
The graph looks like that:
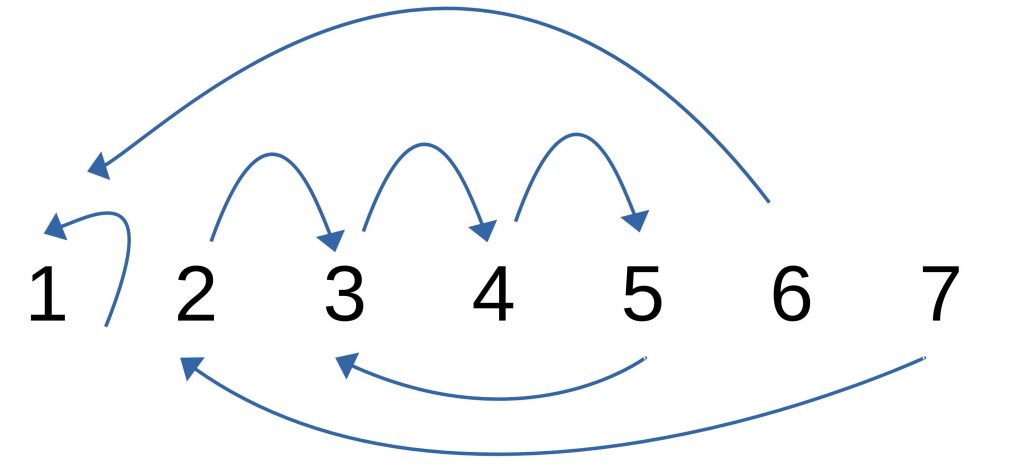
The directed circles are marked yellow.
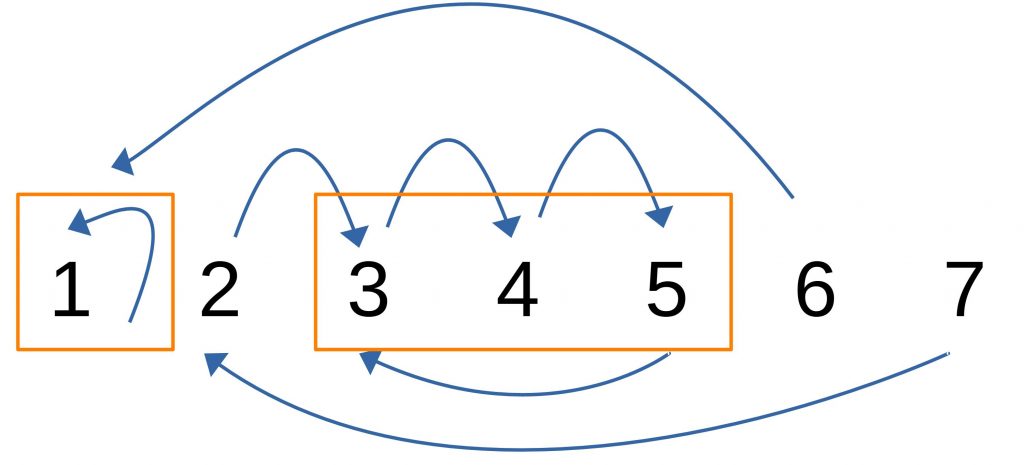
Child 1 prefers its own present over all other presents and “exchanges” this with itself. Children 3, 4, and 5 form a circle. They exchange presents in the opposite direction of the arrows. Child 4 gives the present to child 3, child 5 gives its present to child 4, and child three gives the present to child 5.
Children 1, 3, 4, and 5 are removed from the algorithm. We continue with the second round.
Second round:
| Child | 2 | 6 | 7 | ||||
| 1st choice | 6 | 7 | 6 | ||||
| 2nd choice | 2 | 3 | 3 | ||||
| 3rd choice | 1 | 4 | 1 | ||||
| 4th choice | 7 | 2 | 5 | ||||
| 5th choice | 4 | … | … | ||||
| 6th choice | … | … | |||||
| 7th choice |
Children 6 and 7 are removed from the algorithm. We continue with round three.
Third round:
| Child | 2 | ||||||
| 1st choice | 2 | ||||||
| 2nd choice | 1 | ||||||
| 3rd choice | 7 | ||||||
| 4th choice | 4 | ||||||
| 5th choice | |||||||
| 6th choice | |||||||
| 7th choice |
The circle looks like that:
Result:
- Child 1 receives its own present.
- Child 2 receives its own present.
- Child 3 receives the present of child 4.
- Child 4 receives the present of child 5.
- Child 5 receives the present of child 3.
- Child 6 receives the present of child 7.
- Child 7 receives the present of child 6.
