Nash Equilibrium
In this topic, you will learn what a Nash equilibrium is and how we find it.
Suppose the following situation. We have two players A and B. They live in a small town with a restaurant and a cinema. Both players chose independently whether they go to the restaurant or cinema. They have to decide at the same time but cannot communicate. Hence, they cannot observe the action of the other player.
Each decision yields different utilities for each player depending on the other player’s decision. The following pay-off matrix shows the pay-offs in every situation. The values are chosen at random.
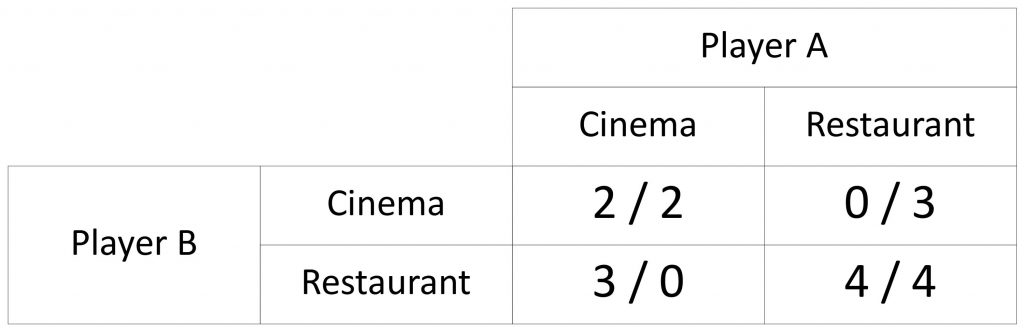
The question is, how should each player decide if no communication between both players is possible?Let’s have a look at player B. If he goes to the cinema and A goes to the cinema too, he receives a pay-off of 2.But if player B goes to the restaurant instead (while A still goes to the cinema) he receives a pay-off of 3.So, if A goes to the cinema, restaurant would be the better choice for B.
Now, let’s consider the situation where player A goes to the restaurant. If player B goes to the cinema, he receives a pay-off of 0. If he goes to the cinema too, he receives 4. So, if A goes to the cinema, again restaurant would be the better choice for B. If we do the same analysis for A, we will find that restaurant is also the best choice.
Apparently, {restaurant, restaurant} is a strategy combination that attracts both players. To figure out if this is a Nash equilibrium, we need to ask the following question: Does any of our players want to abandon this strategy combination unilaterally (= change its decision afterward)? If no player wants to change its decision, we have a Nash equilibrium.
Definition Nash equilibrium:
The best answer to the best answer of the other player.
Or
A Situation where no player wants to change its mind unilaterally.
How to Spot a Nash Equilibrium
The crucial question is, how do we spot a Nash equilibrium in a pay-off matrix? For that purpose, we can use arrows. For every player, we draw an arrow to the best option (the option with the highest reward in this situation). For player B, the arrow goes from cinema to restaurant if player A goes to the cinema. And if player A goes to the restaurant, the arrow goes from cinema to restaurant. You can see this in the following figure.
We do the same for the other player A and receive the following table.
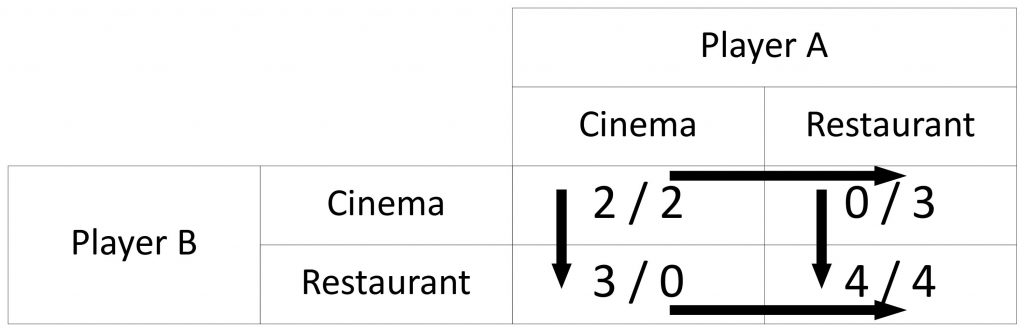
The Nash equilibrium is in the cell, where two arrows point to. In our case, this is the cell {restaurant, restaurant}. If you apply our definition, you will see that neither player B nor player A has an incentive to deviate from this decision unilaterally.
Games With Multiple Nash Equilibria
In the last section, we had only one Nash equilibrium. But some games have more than one. One popular example is the game “battle of the sexes”. Here, players A and B have to decide whether to go to the theater or a football match. If they miss each other, nobody can enjoy the show or the match. If both players spend the evening together in the theater, A receives a pay-off of 1, and A receives 3. If they spend the evening together in the football stadium, A receives a pay-off of 3 and B receives 1.
Let’s consider the following pay-off matrix.
We can see that {Theater, Theater} and {Football, Football} are Nash equilibria.
The consequence is that both players have to coordinate their decisions. But without communication, this is difficult. As a result, it is not sure that the players will reach the Nash equilibrium in such a game!
Games without Nash Equilibrium
There are also games with no Nash equilibrium. Suppose two players, A and B. They have to decide what side of a coin they lay on the table. If both players reveal the same side, player A receives a pay-off of 1 and player B loses 1. If one player reveals heads and the other player tails, A loses 1 and B receives 1.
Let’s consider the following pay-off matrix.
As we can see, there is no Nash equilibrium. Such a game is also called a dis-coordination game as there is no incentive to find a Nash equilibrium.
