Block Validator Selection in PoS
Last Updated on 3. May 2023 by Martin Schuster
There are different schemes how to choose a block validator. Here, we explain
- simple round-robin
- round-robin with stake
- virtual mining rig
Simple Round Robin
The most straightforward scheme is a round robin-block validator selection. Here, block validators register in a list and each validator is chosen in a predefined order. When reaching the end of the list, the selection process starts over.
If you have four validators with the indexes 0, 1, 2, and 3 they would be chosen in this order. And after validator 3 has validated its block, the selection starts with 0 again.
This could be implemented with a modulo calculation.
b % N = i
b: block height: increases with every block
N: number of registered block validators
i: index of the next block validator
%: modulo operation
Example:
We start at block 0
N = 4 (four block validators)
| b | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| b % N = i | 0 | 1 | 2 | 3 | 0 | 1 | 2 | 3 |
But this scheme would not take the number of coins into account. And it would be susceptible to Sybil attacks.
Round Robin with Stake
In order to overcome this issue of Sybil attacks, registration as a voter requires a deposit. One could define a minimum deposit for each index (or slot). If the minimum amount is 2 BTC, then a block validator with a budget of 8 BTC could register for four indexes by distributing its coins evenly.
While the round-robin is easy to implement, it has some downsides. The first is that the order of block validators is predefined which could facilitate coordination between the block validators. And it could also make denial of service attacks easier.
Virtual Mining/Simulated Mining Rig
To overcome the deterministic block validator selection, a random element must be introduced. For this purpose, the following formula can be used:
SHA-256(Hn-1+address+timestamp+R)<= 2^256*(coin_age * deposit)/diff
SHA-256 is a cryptographic hash function.
Hn-1 is the block header of the previous block
address: coinbase address – the address where the block reward goes to or where the stake is deposited
timestamp: timestamp
R: a random value
coin age: (optional) time the coins haven’t been moved
deposit: the amount the block validator has staked on the given address
diff: difficulty parameter
The left side of this inequation must be lower than the target given on the right side. The higher the coin age and the deposit, the easier it is to fulfill the inequation. The higher the difficulty parameter is, the harder it is to solve the puzzle.
The calculation is done in rounds. If no miner was selected, the difficulty parameter gets adjusted and the calculation is repeated. Nxt coin, for example, raises the target every second if no block producer was found.
Without a random element, block producers could engage in stake grinding where other elements like block hash or address are chosen that the inequation in the next round favors this block producer. Calculating the random element is not trivial in a decentralized setup like blockchain. We will explain two different approaches in one of the following topics.
Random shuffling
Random shuffling is similar to a round-robin approach. But the order is determined randomly. This again involves a random element.
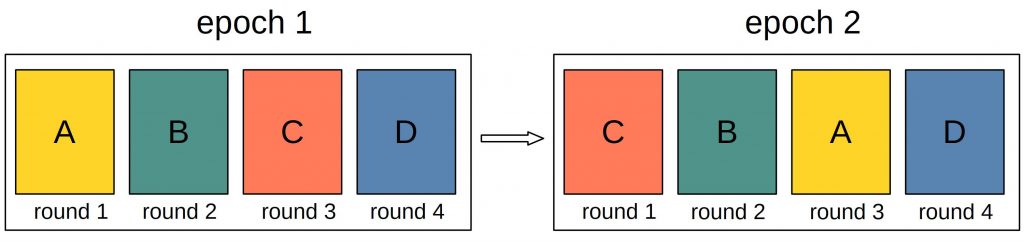
Random shuffling is employed by Ethereum 2.0. It helps to mitigate DoS attacks and collusion among nodes.

 Register
Register Sign in
Sign in