False Positive Rate

Last Updated on 3. May 2023 by Martin Schuster

So far, we learned that bloom filters have a false-positive rate. This rate depends on three parameters:

1. size of the filter in bit (e.g. 8 bit, 32 bit, 256 bit, etc).
2. number of hash functions
3. number of elements included in the bloom filter

We can calculate the probability of a false-positive match with this formula:

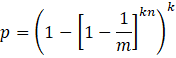
Where

• m: size of the filter in bit
• k: number of hash functions
• n: number of elements in the filter
• p: probability of a false positive match

Numerical Example

Calculate the probability p for a false positive match for the following table:

m	k	n	p
16	3	2
16	3	5
256	3	5
256	10	5
256	200	5

Solution

m	k	n	p
16	3	2	0,03309652
16	3	5	0,238544399
256	3	5	0,000185372
256	10	5	3,14614E-08
256	200	5	0,01772303

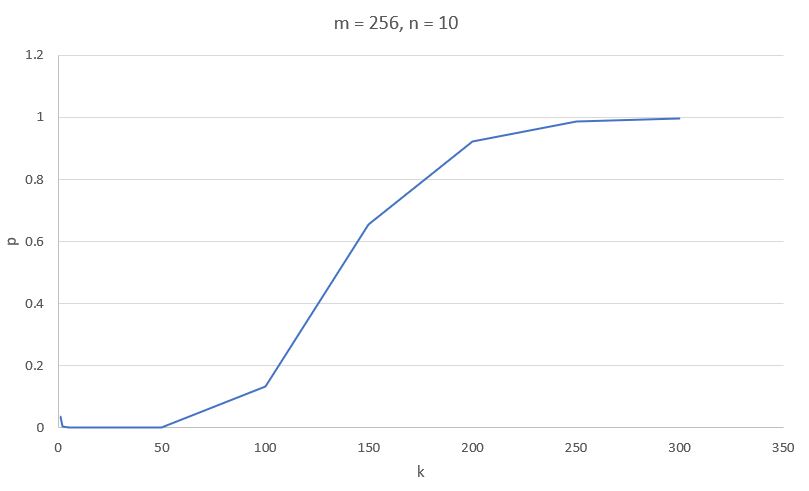
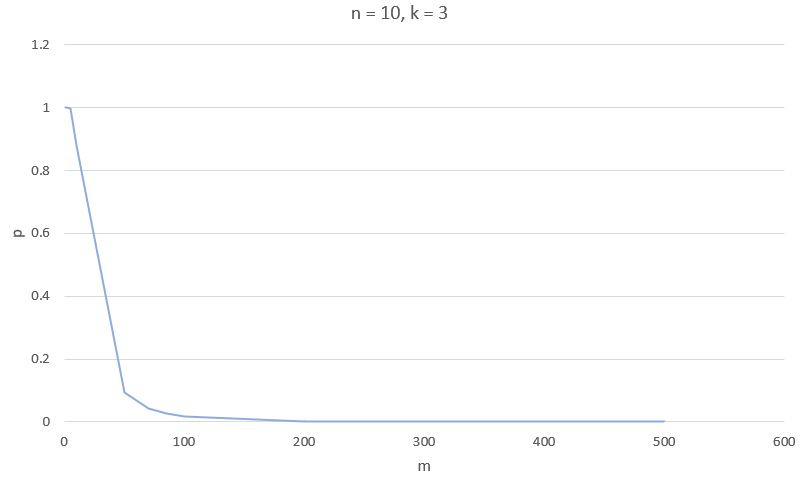
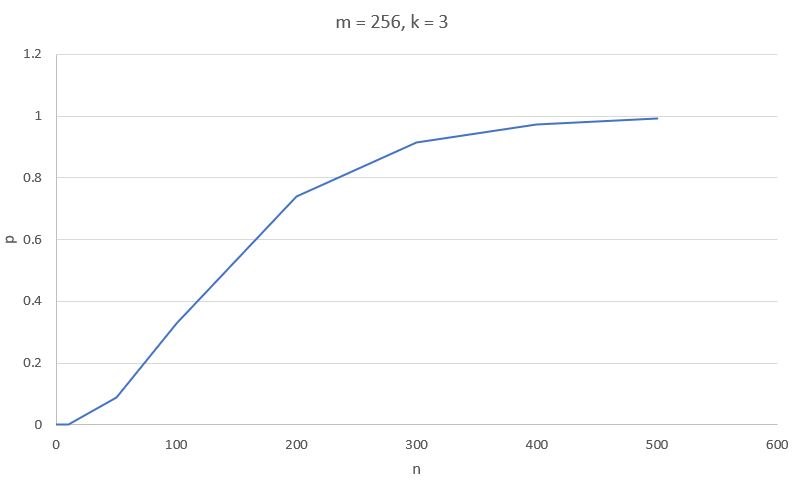
The following charts show the development of false positives depending on m, k, and n if the other parameters are constant.