In this topic, we learn about the data structures used in the Bitcoin Blockchain. The data structures play a vital role in the consensus which is explained later.

You can imagine that there are many transactions in the network. In order to make it easier to deal with them, we put them into so-called blocks. A block basically is a file containing transaction information and a few other data. The following code shows all details that are stored in a block.

{
"hash": "00000000770ebe897270ca5f6d539d8afb4ea4f4e757761a34ca82e17207d886",
"confirmations": 236753,
"strippedsize": 215,
"size": 215,
"weight": 860,
"height": 20000,
"version": 1,
"versionHex": "00000001",
"merkleroot": "01f8255cad4f0060170f5cca22a5e0ca99fa62b3d26b89a34ac3100d876d14a4",
"tx": [{
"txid": "01f8255cad4f0060170f5cca22a5e0ca99fa62b3d26b89a34ac3100d876d14a4",
"hash": "01f8255cad4f0060170f5cca22a5e0ca99fa62b3d26b89a34ac3100d876d14a4",
"version": 1,
"size": 134,
"vsize": 134,
"weight": 536,
"locktime": 0,
"vin": [{
"coinbase": "04ffff001d016b",
"sequence": 4294967295
}],
"vout": [{
"value": 50.00000000,
"n": 0,
"scriptPubKey": {
"asm": "04370295d27dc032142af46515c4251ac7053f947546ada27b530bb11ffc65ea9b81be8758d6218d24448d2f9293620e43cf6e8220da09819d52f85474bc29238a OP_CHECKSIG",
"hex": "4104370295d27dc032142af46515c4251ac7053f947546ada27b530bb11ffc65ea9b81be8758d6218d24448d2f9293620e43cf6e8220da09819d52f85474bc29238aac",
"type": "pubkey"
}}],
"hex": "01000000010000000000000000000000000000000000000000000000000000000000000000ffffffff0704ffff001d016bffffffff0100f2052a01000000434104370295d27dc032142af46515c4251ac7053f947546ada27b530bb11ffc65ea9b81be8758d6218d24448d2f9293620e43cf6e8220da09819d52f85474bc29238aac00000000"
}],
"time": 1248291739,
"mediantime": 1248287332,
"nonce": 2406314246,
"bits": "1d00ffff",
"difficulty": 1,
"chainwork": "00000000000000000000000000000000000000000000000000004e214e214e21",
"nTx": 1,
"previousblockhash": "00000000ba36eb929dc90170a96ee3efb76cbebee0e0e5c4da9eb0b6e74d9124",
"nextblockhash": "000000002434a3edf8dee4fe506d306c59d3bf41f73d979f30ed3f7b7c34d06c"
}

A detailed description of a block can be found here: https://en.bitcoin.it/wiki/Block

For now, we don’t need to understand all fields in a block. For the sake of simplicity, we just consider the block header and the list of transactions.

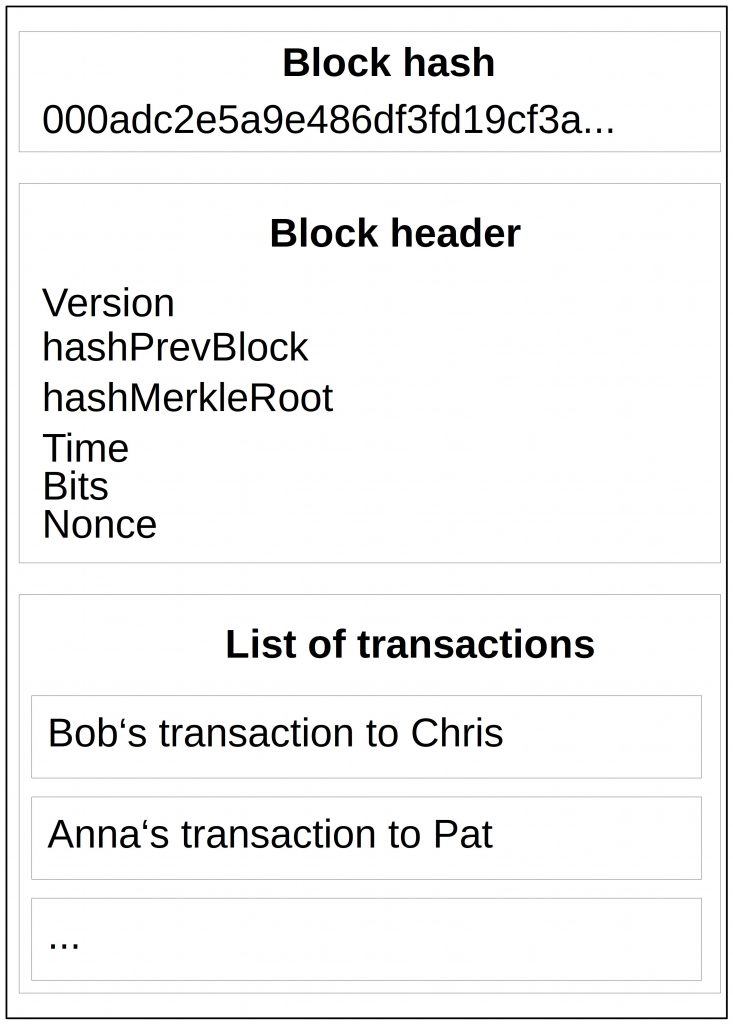
The list of transactions is condensed to a single string by using a Merkle Tree. The Merkle root becomes then part of the block header (in the following it is the field hashMerkleRoot).

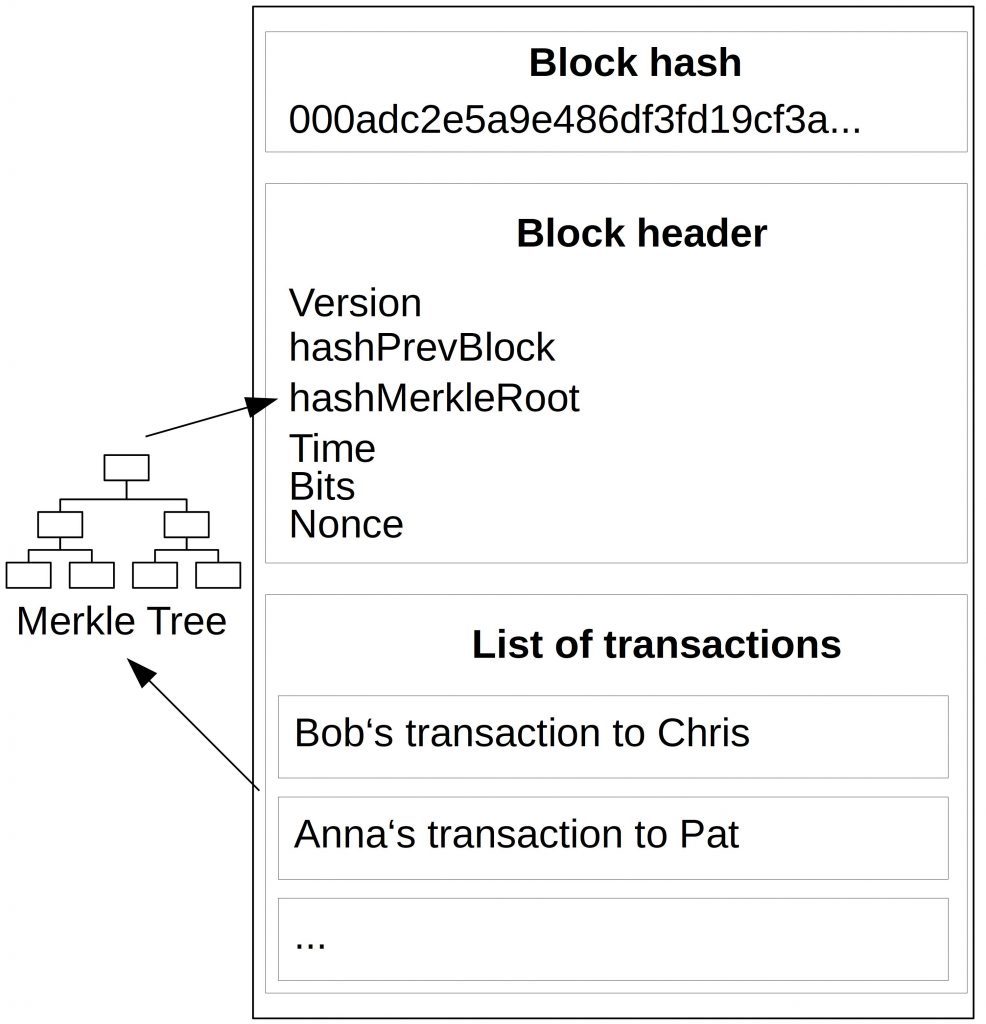
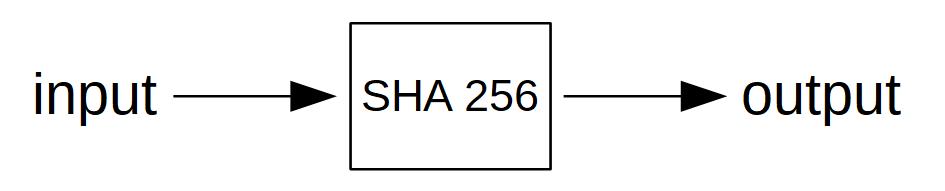
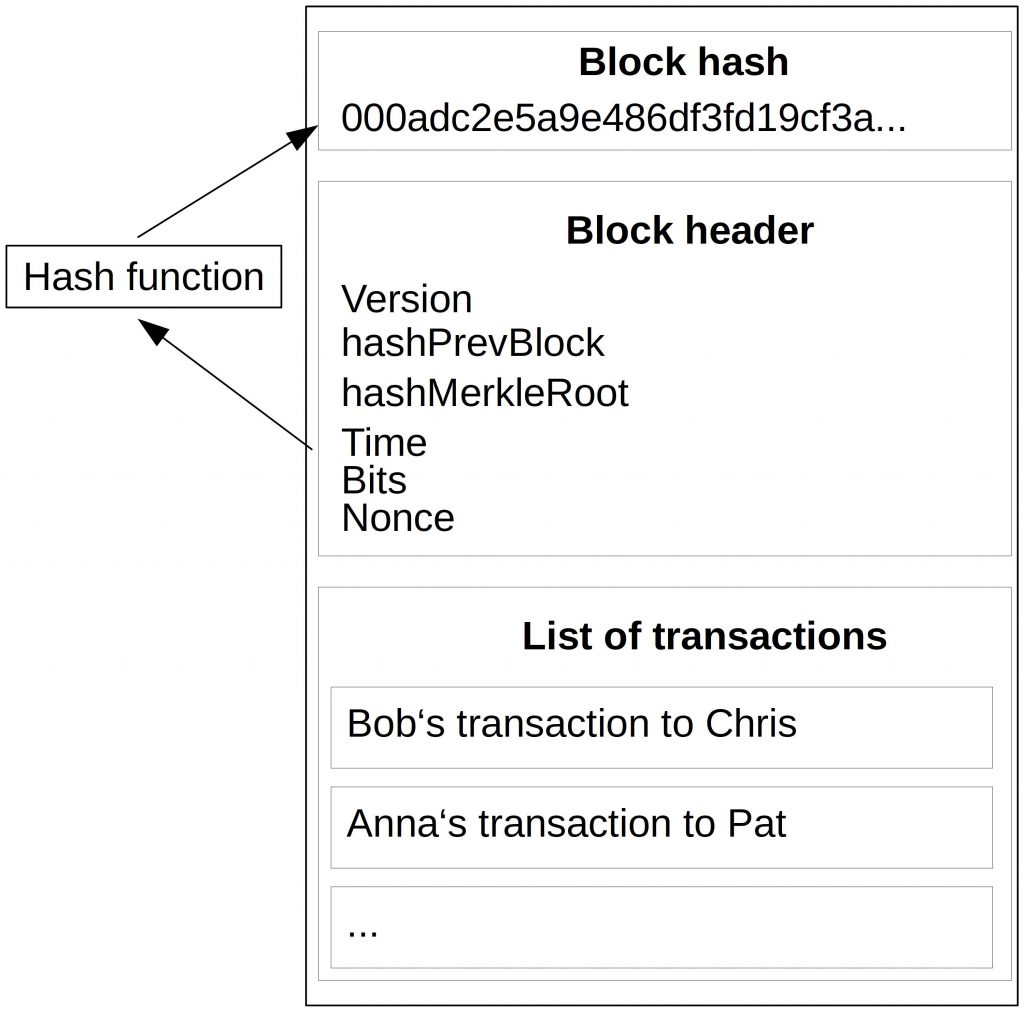
The block header is used as an input of a hash function. A hash function is a mathematical function that takes an input of arbitrary length and condenses it to an output with a fixed length (this output is called digest). There are many hash functions out there. In Bitcoin, we use a hash function called SHA-256. The hash function must belong to a group of cryptographic hash functions. They have stricter security assumptions than other hash functions. You can read more about the requirements of hash functions in cryptocurrencies here.

You can play with some hash functions here to see how they work:

The output looks pretty random to us, and that’s good. There are three important properties:

1. If you use the same input, you always get the same output
2. It is impossible to retrieve the input back from the output (one-way function/hiding property)
3. If you change the input even just a tiny bit the output (hash) changes completely

But for us, this is not enough. We need a cryptographic hash function that has the following properties:

1. Pre-image resistance
2. Second-pre-image resistance
3. Collision resistance
4. Puzzle friendliness

Collision resistance means that it is infeasible to find two different inputs x and y which bring the same output. Of course, there are collisions with every hash function. The reason is that we have an infinite set of inputs but a limited set of outputs. But the output set is still so huge that it takes too long to find such a collision by trying every single input. And there is no shortcut to trying every single input.

The input of our hash function is the data from the block header and the transaction data. Our output hash might look like this: 0x1b49c8ga3627f6…

This hash we write in the head of our block and call it a block hash. You will understand why we need it in the upcoming sections.