Brier Score
Last Updated on 28. April 2023 by Martin Schuster
The Brier Score (BS) is a proper score function that measures the accuracy of a probability prediction.
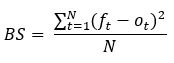
ft: probability that was forecast
ot: actual outcome of the event at instance t
N: Number of forecasting instances
t: instance
The formula above is proper for binary events. So, ot can be 0 (if it doesn’t happen) or 1 (if it happens). The original formula of the Brier score is also applicable for multi-category forecasts.
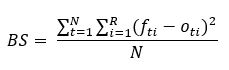
R: number of possible classes in which the event can fall. R = 2 for the case rain / no rain, R = 3 for the case long, normal, short.
N: number of overall instances of all classes
fti: predicted probability of class i
oti: observation for instance t and class i. oti = 1 if this is the ith class, otherwise it is 0.
Interpretation
The Brier score measures the error of the prediction (how far is the prediction away from reality). The lower the Brier score, the better is the prediction. A Brier score of zero would mean that every prediction matched with reality.
Brier Skill Score (BSS)
To interpret the Brier score, it is helpful to compare it with the score of a reference method (baseline method).
A skill score of <0 means that the forecasting method is worse than the reference forecasting method. A skill score of 0 means that it is equivalent and a skill score of >0 means that the forecasting method is better than the reference method. The higher it is, the better the forecast.
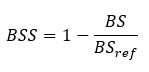
BSref: Brier score for a reference forecasting method.
Often, BSref is calculated for a naïve forecasting method that takes the average probability as a forecast. The average probability is the average of the outcomes o.
Example BSS
| Index | 1 | 2 | 3 | 4 | 5 |
| Event | 0 | 0 | 1 | 1 | 1 |
| Forecasted Probability | 0.1 | 0.2 | 0.6 | 0.8 | 0.9 |
| Square Error with f | 0.01 | 0.04 | 0.16 | 0.04 | 0.01 |
BS = 0.052
The reference model assumes a probability of 0.30 throughout every day.
Henc, it yields a squared error of:
| Square Error with f | 0.09 | 0.09 | 0.49 | 0.49 | 0.49 |
BSref = 0.33
BSS = 0.84242
Advantages and Disadvantages of the Brier Score
+ The Brier Score is easy to calculate
– If the events are rare, the Brier score becomes inaccurate
Example 1
Suppose we have a weather forecast that tries to predict the probability of rain. Since we are only interested in whether it will rain or not, we have a binary decision (rain, no rain). We are only interested in one day (N = 1).
The prediction we want to assess is the probability of rain = 0.9.
In reality, it rained.
Since we have a binary situation, we can use the simplified formula.
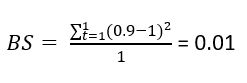
The result of 0.01 is pretty good.
Example 2
Suppose we have a weather forecast that tries to predict the probability of rain. Since we are only interested in whether it will rain or not, we have a binary decision (rain, no rain). We are interested in five days (N = 5).
| Day | 1 | 2 | 3 | 4 | 5 |
| Prediction | 0.9 | 0.7 | 0.5 | 0.4 | 0.1 |
| Reality | 1 | 1 | 0 | 1 | 0 |
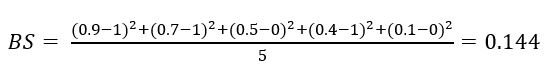

 Register
Register Sign in
Sign in