Bayes/Conditional Probability
Last Updated on 28. April 2023 by Martin Schuster
While the confusion matrix is easy to understand, it is helpful to get a more general equation to calculate the likelihood of conditional events.
The formula for that is:
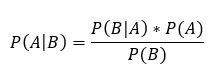
P(A|B): Conditional Probability that event A occurs under the condition that B has occurred.
P(B|A): Conditional Probability that event B occurs under the condition that A has occurred.
P(A): Probability that event A occurs.
P(B): Probability that event B occurs.
Example
Suppose we have three treasure boxes. In each box are two coins. This could be either a silver coin (S) or a gold coin (G). The following list shows how the coins are distributed among the boxes.
Box 1: GG
Box 2: GS
Box 3: SS
If we randomly select a box and draw a gold coin from it blindly, what is the likelihood of selecting box 1?
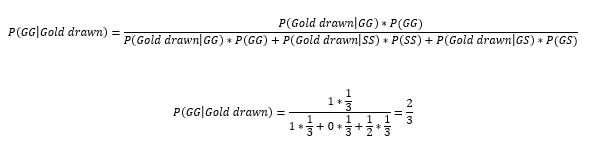

 Register
Register Sign in
Sign in